TRI Author: Soonho Kong
All Authors: Calvin Huang, Soonho Kong, Sicun Gao, and Damien Zufferey
Interval Constraint Propagation (ICP) is a powerful method for solving general nonlinear constraints over real numbers. ICP uses interval arithmetic to prune the space of potential solutions and, when the constraint propagation fails, divides the space into smaller regions and continues recursively. The original goal is to find paving boxes of all solutions to a problem. Already when the whole domain needs to be considered, branching methods do matter much. However, recent applications of ICP in decision procedures over the reals need only a single solution. Consequently, variable ordering in branching operations becomes even more important.
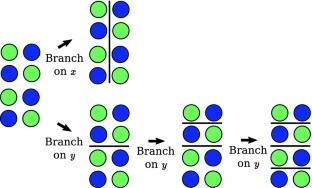
In this work, we compare three different branching heuristics for ICP. The first method, most commonly used, splits the problem in the dimension with the largest lower and upper bound. The two other types of branching methods try to exploit an integration of analytical/numerical properties of real functions and search-based methods. The second method, called smearing, uses gradient information of constraints to choose variables that have the highest local impact on pruning. The third method, lookahead branching, designs a measure function to compare the effect of all variables on pruning operations in the next several steps.
We evaluate the performance of our methods on over 11,000 benchmarks from various sources. While the different branching methods exhibit significant differences on larger instance, none is consistently better. This shows the need for further research on branching heuristics when ICP is used to find an unique solution rather than all solutions. Read more
Citation: Huang, Calvin, Soonho Kong, Sicun Gao, and Damien Zufferey. "Evaluating Branching Heuristics in Interval Constraint Propagation for Satisfiability." In International Workshop on Numerical Software Verification, pp. 85-100. Springer, Cham, 2019.