TRI Authors: Hongkai Dai, Russ Tedrake
All Authors: Hongkai Dai, Gregory Izatt, Russ Tedrake
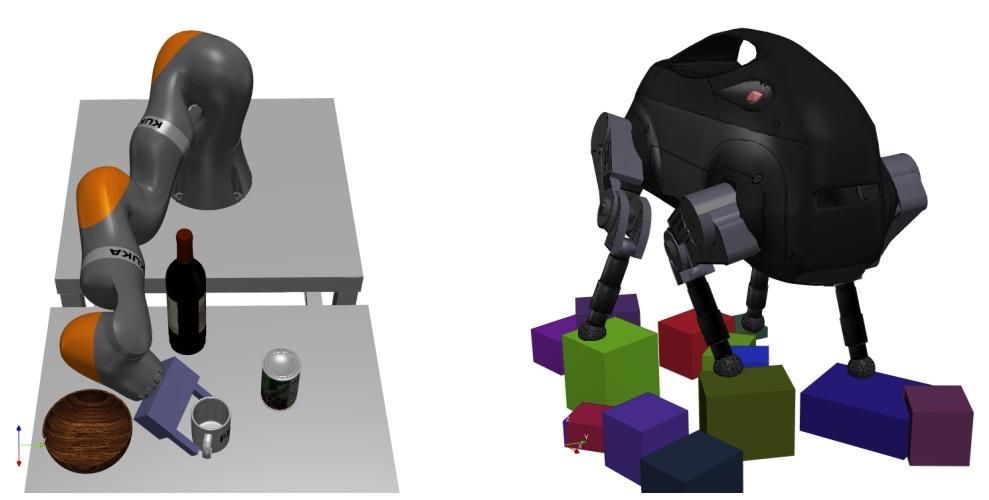
In this paper, we present a novel formulation of the inverse kinematics (IK) problem with generic constraints as a mixed-integer convex optimization program. The proposed approach can solve the IK problem globally with generic task space constraints: a major improvement over existing approaches, which either solve the problem in only a local neighborhood of the user initial guess through nonlinear non-convex optimization, or address only a limited set of kinematics constraints. Specifically, we propose a mixed-integer convex relaxation of non-convex SO(3) rotation constraints, and apply this relaxation on the IK problem. Our formulation can detect if an instance of the IK problem is globally infeasible, or produce an approximate solution when it is feasible. We show results on a seven-joint arm grasping objects in a cluttered environment, an 18-degree-of-freedom quadruped standing on stepping stones, and a parallel Stewart platform. Moreover, we show that our approach can find a collision free path for a gripper in a cluttered environment, or certify such a path does not exist. We also compare our approach against the analytical approach for a six-joint manipulator. The open-source code is available at http://drake.mit.edu. Read More
Citation: Dai, Hongkai, Gregory Izatt, and Russ Tedrake. "Global inverse kinematics via mixed-integer convex optimization." The International Journal of Robotics Research 38, no. 12-13 (2019): 1420-1441.