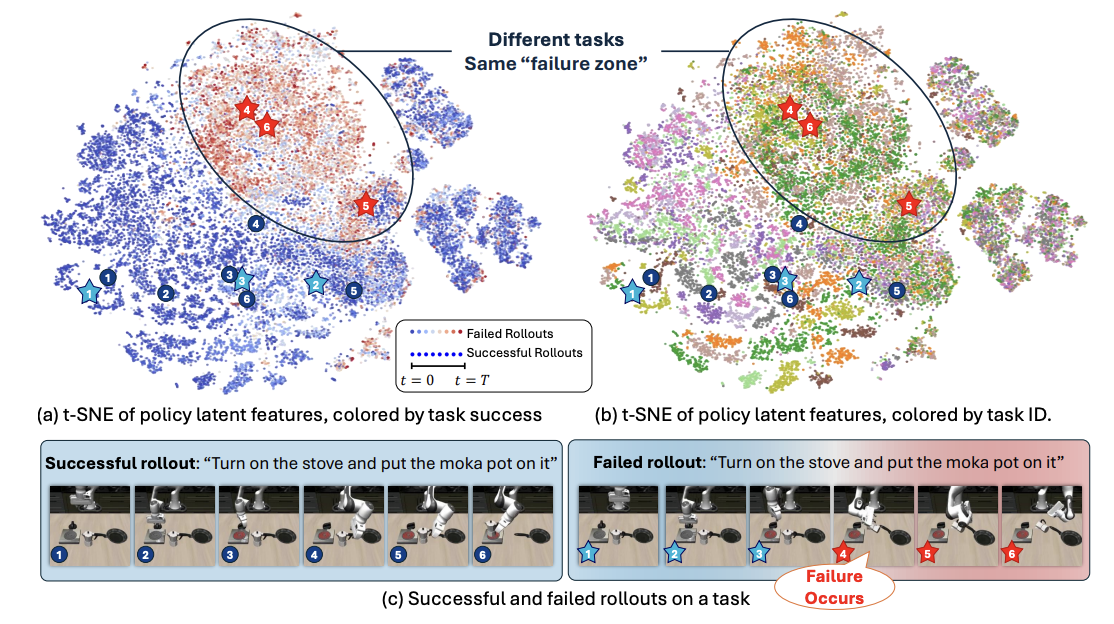
TRI Author: Hongkai Dai

All Authors: Romeo Orsolino, Michele Focchi, Carlos Mastalli, Hongkai Dai, Darwin G. Caldwell and Claudio Semini

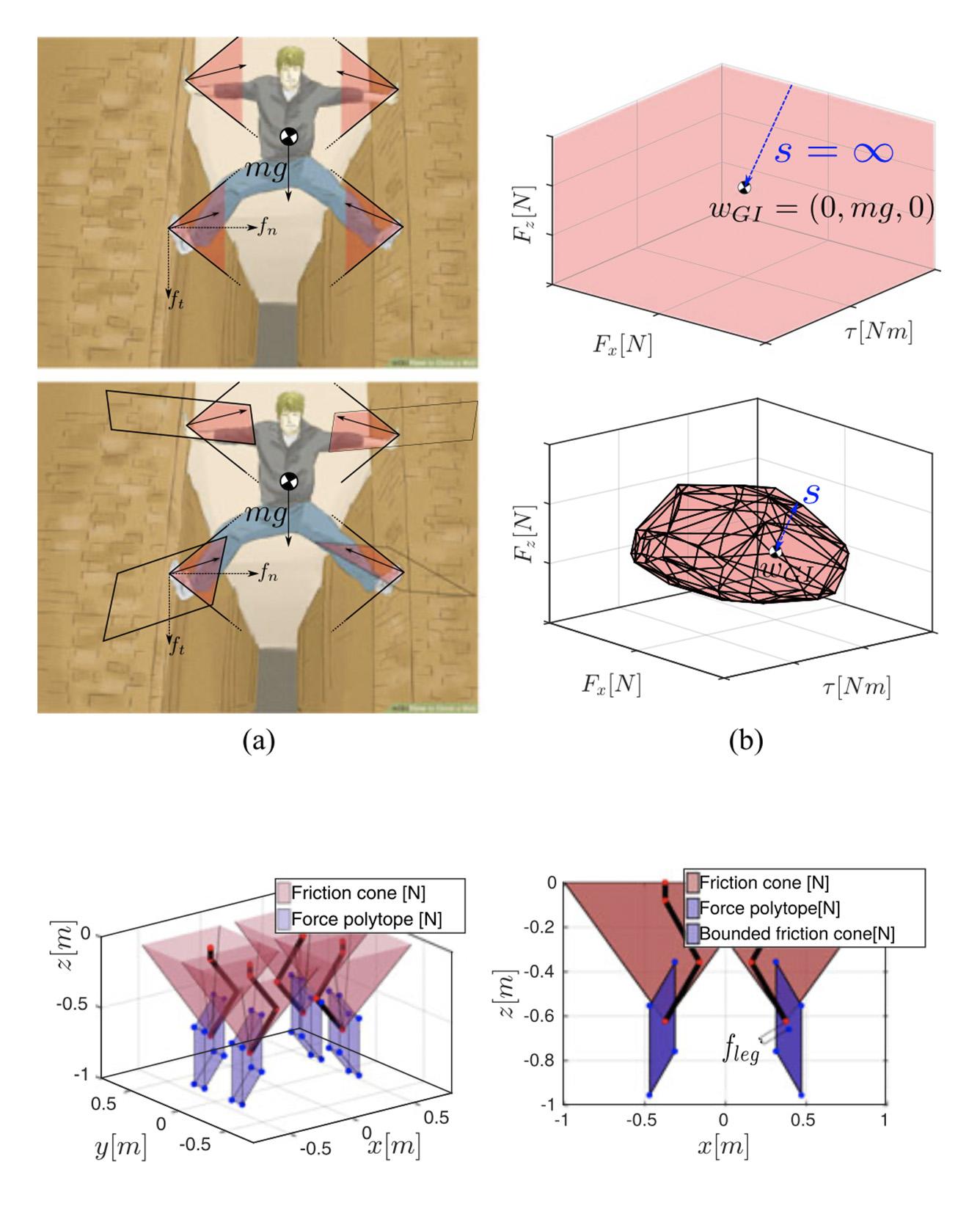
Motion planning in multicontact scenarios has recently gathered interest within the legged robotics community, however actuator force/torque limits are rarely considered. We believe that these limits gain paramount importance when the complexity of the terrains to be traversed increases. We build on previous research from the field of robotic grasping to propose two new six-dimensional bounded polytopes named the Actuation Wrench Polytope (AWP) and the Feasible Wrench Polytope (FWP). We define theAWP as the set of all the wrenches that a robot can generate while considering its actuation limits. This considers the admissible contact forces that the robot can generate given its current configuration and actuation capabilities. The Contact Wrench Cone (CWC) instead includes features of the environment such as the contact normal or the friction coefficient. The intersection of the AWP and of the CWC results in a convex polytope, the FWP, which turns out to be more descriptive of the real robot capabilities than existing simplified models, while maintaining the same compact representation. We explain how to efficiently compute the vertex-description of the FWP that is then used to evaluate a feasibility factor that we adapted from the field of robotic grasping. This allows us to optimize for robustness to external disturbance wrenches. Based on this, we present an implementation of a motion planner for our quadruped robot HyQ that provides online Center of Mass trajectories that are guaranteed to be statically stable and actuation-consistent. Read More

Citation: Orsolino, Romeo, Michele Focchi, Carlos Mastalli, Hongkai Dai, Darwin G. Caldwell, and Claudio Semini. "Application of wrench-based feasibility analysis to the online trajectory optimization of legged robots." IEEE Robotics and Automation Letters 3, no. 4 (2018): 3363-3370.